Первісна та інтеграл

Первісна

Для знаходження функції за її похідною застосовують операцію інтегрування, обернену до операції диференціювання.

Якщо для всіх \(x\) із заданого проміжку \([a; b]\)

то \(F(x)\) називається первісною для \(f(x)\) на цьому проміжку.

Загальний вигляд первісних для функції \(f(x)\) на проміжку \([a; b]\) є \(F(x)+C\), де \(C\) — довільна стала, а \(F(x)\) — одна з первісних для \(f(x)\) на проміжку \([a; b]\).

Правила знаходження первісних

1. Якщо \(F(x)\) — первісна для \(f(x)\), а \(G(x)\) — первісна для \(g(x)\), то \(F(x)+G(x)\) — первісна для \(f(x)+g(x)\).
2. Якщо \(F(x)\) — первісна для \(f(x)\), а \(k\) — стала, то \(k \cdot F(x)\) — первісна для \(k \cdot f(x)\).
3. Якщо \(F(x)\) — первісна для \(f(x)\), а \(k ~ (k \ne 0)\) і \(b\) — сталі, то \(\frac{1}{k} \cdot F(kx+b)\) — первісна для \(f(kx+b)\).

Площа криволінійної трапеції

Нехай на відрізку \([a; b]\) осі \(Ox\) задано неперервну функцію \(f(x)\), яка не змінює на ньому знак. Фігуру, обмежену графіком цієї функції, відрізком \([a; b]\), прямими \(x=a\) і \(x=b\) (рис. 1), називають криволінійною трапецією.

Рис.1. Площа криволінійної трапеції.

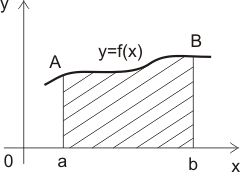
Площа криволінійної трапеції \(aABb\) (рис. 1), обмежена віссю \(Ox\), прямими \(x=a\) і \(x=b\) та графіком невід’ємної функції \(y=f(x)\) на відрізку \([a; b]\), визначається за формулою

Якщо функція \(f(x)\) неперервна і невід’ємна на відрізку \([a; b]\) і \(F(x)\) — первісна для \(f(x)\) на відрізку \([a; b]\), то площу \(S\) криволінійної трапеції знаходять за формулою Ньютона-Лейбніца:

Коли неперервна функція \(f(x) \leq 0\) на \([a; b]\), то обчислити площу відповідної криволінійної трапеції можна за формулою:

Якщо фігура обмежена графіками двох неперервних функцій \(f_1(x)\) та \(f_2(x)\) і двома прямими \(x=a\) і \(x=b\), де \(f_1(x) \geq f_2(x)\) на відрізку \([a; b]\), то площу такої фігури шукають за формулою: