Бер 4, 2012 о 14:19 | Автор: admin
У 1938 році американський математик Едвард Каcнер гуляв по парку з двома своїми племінниками і обговорював з ними великі числа. В ході розмови зайшла мова про число зі ста нулями (10100), у якого не було власної назви. Один із племінників, дев'ятирічний Мілтон Сіротта, запропонував назвати це число «гугол» (googol).
Читати далі »
Лют 25, 2012 о 15:14 | Автор: admin
Microsoft Mathematics 4.0 являє собою графічний калькулятор, що будує двовимірні та тривимірні графіки, забезпечує покрокове розв’язання рівнянь, надає доступ до корисних інструментів, призначених для розв’язання математичних задач, а також задач з інших предметів.

Використовуючи дану програму учні мають нагоду навчитися розв’язувати рівняння крок за кроком, отримати кращі уявлення про основи алгебри, тригонометрії, математичних обчислень, фізики та хімії.
Читати далі »
Лют 25, 2012 о 14:23 | Автор: admin
Для більшості сучасних людей термін «софісти» незрозумілий, і це не дивно. Софістами називали викладачів наук і мистецтва ще у Стародавній Греції. Це був своєрідний напрямок філософів. Навіть сама їх назва в перекладі з грецької мови означає «ті, що мудрують».
Софісти були універсальними вчителями, які навчали всіх бажаючих мудрості. У ті часи вважалося, що навчання має бути побудоване не на отриманні знань, а на вмінні міркувати.
На початковому етапі софістика була просвітницького характеру, однак, її основою були принципи, які породили марнослів'я. Згодом софістика стала особливим вченням про те, як правильно спростовувати або захищати будь-яке положення. Люди почали вивчати ряд практичних прийомів, заснованих на використанні тавтологій. В ті часи з'явилася гра слів, які не мали сенсу і, звичайно ж, міркування, так звані софізми.
Читати далі »
Січ 21, 2012 о 17:53 | Автор: admin
Якісно нові факти, нагромаджені в математиці наприкінці XVIII — початку XIX ст., виняткова роль, яку почали відігравати комплексні числа в науці і техніці, сприяли тому, що метафізичний підхід до математики став несумісним з розвитком учення про число, алгебри, аналізу нескінченно малих і геометрії.
Вперше геометричне тлумачення комплексних чисел як векторів на площині дав уродженець Норвегії, датський математик і землемір Каспар Вессель (1745—1818) у своїй книзі «Про аналітичне подання напрямів» (1799).
Читати далі »
Січ 21, 2012 о 15:03 | Автор: admin

Додаткові курси зі шкільних предметів, послуги репетитора, факультативи для школярів — всі вони затребувані на даний час. І незважаючи на складний час, потік батьків, які збираються підшукати для своєї дитини викладача з того чи іншого предмету, не зменшується.
На загальних уроках педагог орієнтується на якийсь абстрактний середній рівень знань своїх учнів. Саме тому той, хто раніше вчився слабше, може багато в чому відставати від інших учнів. І, кінцевий результат цих занять буде не таким, як очікувалось.
Читати далі »
Гру 10, 2011 о 16:57 | Автор: admin

Чому Нобелівська премія не вручається за досягнення в математиці?
Існує думка, що Альфред Нобель не включив математику в список дисциплін своєї премії через те, що його дружина зрадила його з математиком. Насправді Нобель ніколи не був одружений. Справжня причина ігнорування математики Нобелем невідома, але є кілька припущень. Наприклад, на той момент вже існувала премія з математики від шведського короля. Інша — математики не роблять важливих винаходів для людства, так як ця наука має чисто теоретичний характер.
Читати далі »
Гру 6, 2011 о 20:41 | Автор: admin
Нещодавно, 5 грудня, на офіційному блозі пошукової системи Google, Аді Авідор (інженер і любитель математики), повідомив про новий цікавий для нас з вами функціонал.
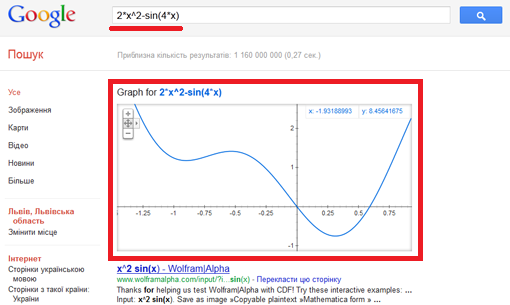
Читати далі »
Лис 12, 2011 о 21:08 | Автор: admin

Як гадаєте, що важче: тонна дерева чи тонна заліза? Не поспішайте відповідати, що вага в обох випадках однакова — подумайте як слід!
Читати далі »
Жов 29, 2011 о 16:02 | Автор: admin
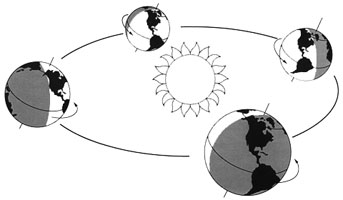
Щоб знайти кількість днів у році треба період обертання Землі навколо Сонця поділити на період обертання Землі навколо власної осі. Оскільки ми ведемо спостереження із Землі, що бере участь в декількох нерівномірних обертання, то експериментально визначити періоди обертань непросто, більш того — вони будуть непостійними.
Читати далі »
Жов 29, 2011 о 15:10 | Автор: admin
(Математики жартують)

Троє математиків і троє фізиків збираються їхати на поїзді в інше місто на конференцію. Вони зустрічаються перед касою на вокзалі. Першою підходить черга фізиків і вони, як усі нормальні люди купують по квитку на людину. Математики ж купують один квиток на всіх.
«Як же так?» — Дивуються фізики — «Адже в поїзді контролер, вас же без квитків звідти виженуть!».
«Не хвилюйтеся» — відповідають математики — «У нас є МЕТОД».
Читати далі »






